１．はじめに

後藤はタバコの適正価格を600円と算出している。しかし、彼の用いたデータ、および社会コスト、経済メリットの定義を用いて計算しても、真の適正価格は1000円となるはずである。
１）　後藤は、社会費用＝経済メリット、を満たす価格を適正価格として算出しているのであるが、それは不適当であり、経済メリットと社会的費用の差を最大にする価格が真の適正価格である。
２）　さらに、後藤は賃金支払いを経済メリットとしている。しかし、労働者は労働サービスを提供してその対価として賃金を受けているのであるから、賃金総額そのものが経済メリットではない。経営者にとっては、売り上げそのものが経済メリットではなく、売り上げから費用を差し引いた利潤が経済メリットであるのと同様である。労働者の場合、費用に相当するのは、労働提供に伴う苦痛であるが、これは測定困難である。とりあえずは、労働者にとっては、賃金は彼らの労働の苦痛をちょうど補償するだけの金額であったと仮定して、経済メリットのなかに賃金を含めずに計算してみることにする。
３）　また、タバコ消費によって、喫煙者が感じる純メリットは、タバコ価格を超える心理的メリットである。これは需要曲線を特定しているのであるから測定できる。しかし、タバコが周囲にもたらす非喫煙者の心理的迷惑を測定し算入しない以上、喫煙者の心理的メリットを算入するわけにはいかない。後藤はこの双方ともに算入していない。これに従う。
４）　タバコの社会的コストのうち、販売量に比例するのは清掃費用のみ、と後藤は考えているが、医療費などすべての費用が販売量に依存すると考えるべきである。

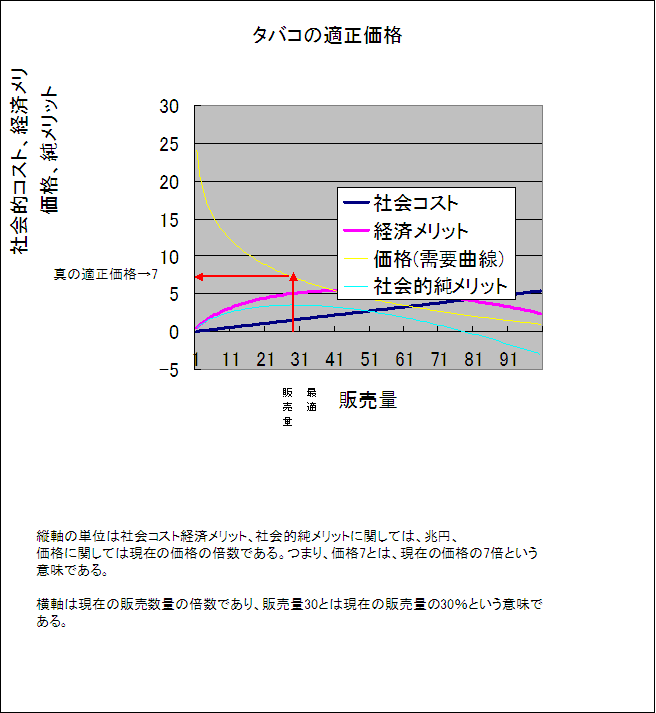
以上の方針に従って計算すると、適正価格は、現在の7倍であり、1400円と導出される。

２．導出方法

1990年の資料によると，タバコ産業は総額2.8兆円のメリットを生み出した．その内訳は，税金納付1.9兆円，タバコ産業賃金，内部留保0.4兆円，経済波及効果による他産業での賃金支払い0.2兆円，他産業での内部留保0.3兆円．社会的コストは医療費3.2兆円，喪失国民所得2兆円，消防・清掃費用0.2兆円，合計5.6兆円である [1]．
このデータを基に後藤はタバコの適正価格を以下のようにして求めている．まずは、後藤の導出方法を説明する。
社会コスト5.6兆円のうち，消防清掃費用のみ相対需要に比例するとし，後は固定費と考え，

社会コスト＝5.4+0.2Q

とする．Qは生産量である。なお，この時点での価格，需要量をそれぞれ１と基準化している．経済メリット2.8兆円は相対価格・相対需要に比例するとして

経済メリット＝2.8ｐQ

とする．ｐは価格である。最適価格とは

社会コスト＝経済メリット

を成立させる価格であるとしている．なお，タバコ需要の価格弾力性は0.2として推計しているので，その需要関数をQ=exp(−0.2（ｐ−１）)とおく [2]．その結果，最適価格は約3であると導出している．よって，タバコの適正価格は現在の３倍であり，約600円であると．

冒頭の挙げた１）に述べたように、これは論理のミスであり、同じ資料および同じ社会コスト社会的メリットの定義を用いても、適正価格は600円ではなく、1000円となる。

純経済メリット＝経済メリット―社会コスト

が最大となるところが、社会的最適である。後藤の定義では、純経済メリット は

W=2.8p・exp(−0.2（ｐ−１）)−5.4−0.2ｐ・exp(−0.2（ｐ−１）)

であるから，この値の に関する最大は ＝5のときに実現され [3]，よって，現在のタバコ価格の約5倍，つまり，1000円が適正価格となる．
　しかし、これも適切な計算方法ではなく、冒頭に挙げた２）、３）、４）の方針によって計算すると次のようになる。賃金支払いを除いて経済メリットを計算すると、2.44ｐQとなり、また、社会的コストは、清掃費用のみならず、すべての費用がタバコの販売量に比例すると考えると、5.4Qとなる。 よって最大化するべき純社会メリットは

W=2.44p・exp(−0.2（ｐ−１）)−5.4Q

となり、これはQ=0.3、ｐ＝7で最大化される。よって、タバコの適正価格は現行の7倍であり、1400円である。

---